diagrama de dispersión

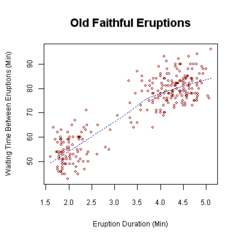Un diagrama de dispersión o gráfica de dispersión o gráfico de dispersión es un tipo de diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables para un conjunto de datos. Los datos se muestran como un conjunto de puntos, cada uno con el valor de una variable que determina la posición en el eje horizontal (x) y el valor de la otra variable determinado por la posición en el eje vertical (y).

características 

Los diagramas de dispersión se emplean para:

• Observar el grado de intensidad en la relación entre dos variables, esta relación puede ser entre un efecto y una de las supuestas causas que lo producen o para ver la relación entre dos causas que provocan un mismo efecto.
• Visualizar rápidamente cambios anómalos.
• Analizar determinadas cuestiones mediante comparaciones.

Modo de aplicación

Los pasos a seguir para construir un diagrama de dispersión son:

1. Seleccionar las 2 variables que se van relacionar.
2. Establecer una hipótesis de la posible relación entre ambas.
3. Construir una tabla que nos relacione los valores de ambas variables por parejas. Si no disponemos de dichos datos será necesario realizar una toma.
4. Dibujar el diagrama poniendo una variable en cada uno de los ejes cartesianos (x,y) con una escala de valores que se ajuste a los datos que se dispone.
5. Representar en el gráfico cada par de valores por un punto.
6. Encontrar la correlación analizando la tendencia de la nube de puntos y la correlación entre las variables.

Hoy en día gracias a la informática disponemos de programas basados en hojas de cálculo como Excel, Numbers o Calc que te permiten realizar rápidamente un diagrama de dispersión con solo introducir los datos de las variables.

Interpretación del diagrama de dispersión

Una vez que hemos realizado el diagrama de dispersión la forma que adquiera la nube de puntos nos permitirá analizar la relación entre las 2 variables o grupos de datos, pudiendo obtener las siguientes figuras e interpretaciones:

• Correlación positiva - Se observa como la nube de puntos obtenida adquiere una forma de recta creciente, cuando los puntos de la nube se encuentra próximos a la recta se le conoce como fuerte, en el caso que se encuentren distantes a la recta es conocida como débil. Por ejemplo la relación existente entre la altura y el peso de una persona es positiva a mayor altura mayor peso.
• Correlación negativa - Al contrario del caso anterior se observa como la nube de puntos obtenida adquiere una forma de recta decreciente, cuando los puntos de la nube se encuentra próximos a la recta se le conoce como fuerte, en el caso que se encuentren distantes a la recta es conocida como débil. Por ejemplo la relación existente para los fumadores entre el número de paquetes de tabaco al mes y los años de vida es negativa dado que a mayor cantidad de tabaco fumado menor esperanza de vida.
• Correlación compleja - La nube de puntos obtenidas adquiere forma de curva, elipse u otra forma geométrica.
• Correlación nula - Se observa una distribución de la nube de puntos con una forma circular, indicándonos la no existencia de relación entre ambas variables. Por ejemplo la relación existente entre el color de los ojos y el tamaño del pie es nula.
• ejemplos 

      

  cuestionario:

  1.- ¿que es un diagrama de dispersión?

  R= Es un tipo de diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables para un conjunto de datos.

  
  

  2.- ¿para que se emplean?

  R= Observar el grado de intensidad en la relación entre dos variables, esta relación puede ser entre un efecto y una de las supuestas causas que lo producen o para ver la relación entre dos causas que provocan un mismo efecto.

  Visualizar rápidamente cambios anómalos.

  Analizar determinadas cuestiones mediante comparaciones.

  
  

  3.- ¿cuantos modos de aplicación existen?

  R= 6

  
  

  4.- ¿como elaborar un diagrama de dispersion?

  R= 

  1. Obtener tabla de pares de valores con valores máximos y mínimos de cada variable.
  2. Situar la causa sospechada en el eje horizontal.
  3. Dibujar y rotular los ejes horizontales y verticales.
  4. Trazar el área emparejada usando círculos concéntricos en pares de datos idénticos
  5. Poner título al gráfico y rotular.
  6. Identificar y clasificar el modelo de correlación.
  7. Comprobar los posibles fallos en el análisis.